662. 二叉树最大宽度

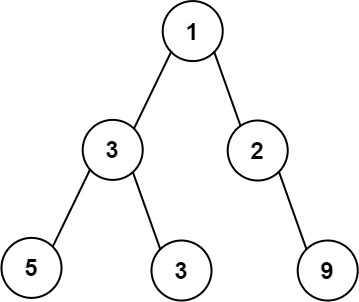
https://leetcode.cn/problems/maximum-width-of-binary-tree/ 给你一棵二叉树的根节点 root ，返回树的最大宽度。树的最大宽度是所有层中最大的宽度。每一层的宽度被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。题目数据保证答案将会在 32 位带符号整数范围内。示例 1：
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。
示例 2：
输入：root = [1,3,2,5,null,null,9,6,null,7]
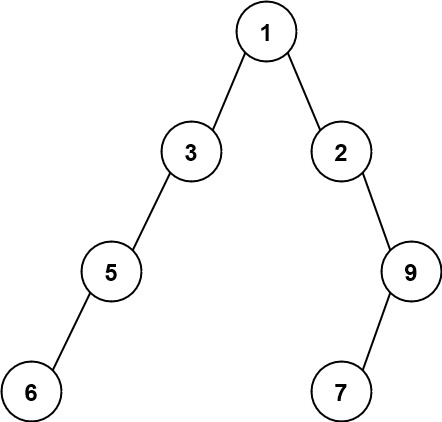
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。
示例 3：
输入：root = [1,3,2,5]
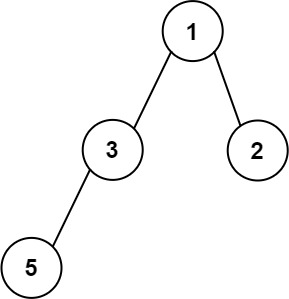
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。
提示：

\(树中节点的数目范围是 [1, 3000]\)

\(-100<=Node.val<=100\)

# 题解

解法一：广度优先遍历（官方题解）


class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        unsigned long long res = 1;
        vector<pair> arr;
        arr.emplace_back(root, 1L);
        while (!arr.empty()) {
            vector<pair> tmp;
            for (auto &[node, index] : arr) {
                if (node->left) {
                    tmp.emplace_back(node->left, index * 2);
                }
                if (node->right) {
                    tmp.emplace_back(node->right, index * 2 + 1);
                }
            }
            res = max(res, arr.back().second - arr[0].second + 1);
            arr = move(tmp);
        }
        return res;
    }
};

复杂度分析：

时间复杂度：\(O (n)\)
空间复杂度：\(O (n)\)

解法二：深度优先遍历（官方题解）

using ULL = unsigned long long;

class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        unordered_map<int, ULL> levelMin;
        function<ULL(TreeNode*, int, ULL)> dfs = [&](TreeNode* node, int depth, ULL index)->ULL {
            if (node == nullptr) {
                return 0LL;
            }
            if (!levelMin.count(depth)) {
                levelMin[depth] = index; // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
            }
            return max({index - levelMin[depth] + 1LL, dfs(node->left, depth + 1, index * 2), dfs(node->right, depth + 1, index * 2 + 1)});
        };
        return dfs(root, 1, 1LL);
    }
};