# 864. 获取所有钥匙的最短路径

给定一个二维网格 grid ，其中：

‘.’ 代表一个空房间
‘#’ 代表一堵
‘@’ 是起点
小写字母代表钥匙
大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为钥匙 / 锁的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

示例 1：

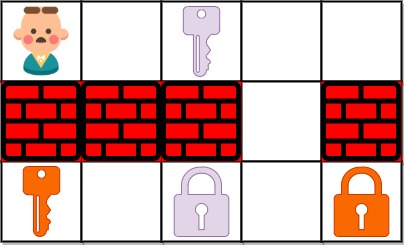
输入：grid = ["@.a.#","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

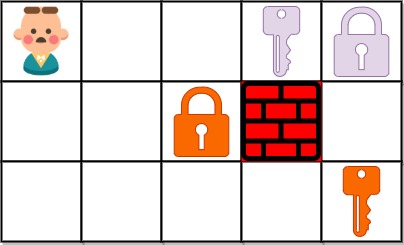
输入：grid = ["@..aA","..B#.","....b"]
输出：6

示例 3:

输入: grid = ["@Aa"]
输出: -1

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 30
grid [i][j] 只含有 ‘.’, ‘#’, ‘@’, ‘a’-‘f’ 以及 ‘A’-‘F’
钥匙的数目范围是 [1, 6]
每个钥匙都对应一个不同的字母
每个钥匙正好打开一个对应的锁

# 题解

class Solution {
public:
    int shortestPathAllKeys(vector<string>& grid) {
        int m = grid.size(), n = grid[0].size();
        int sx = 0, sy = 0;
        unordered_map<char, int> key_to_idx;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == '@') {
                    sx = i;
                    sy = j;
                }
                else if (islower(grid[i][j])) {
                    if (!key_to_idx.count(grid[i][j])) {
                        int idx = key_to_idx.size();
                        key_to_idx[grid[i][j]] = idx;
                    }
                }
            }
        }

        queue<tuple<int, int, int>> q;
        vector<vector<vector<int>>> dist(m, vector<vector<int>>(n, vector<int>(1 << key_to_idx.size(), -1)));
        q.emplace(sx, sy, 0);
        dist[sx][sy][0] = 0;
        while (!q.empty()) {
            auto [x, y, mask] = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] != '#') {
                    if (grid[nx][ny] == '.' || grid[nx][ny] == '@') {
                        if (dist[nx][ny][mask] == -1) {
                            dist[nx][ny][mask] = dist[x][y][mask] + 1;
                            q.emplace(nx, ny, mask);
                        }
                    }
                    else if (islower(grid[nx][ny])) {
                        int idx = key_to_idx[grid[nx][ny]];
                        if (dist[nx][ny][mask | (1 << idx)] == -1) {
                            dist[nx][ny][mask | (1 << idx)] = dist[x][y][mask] + 1;
                            if ((mask | (1 << idx)) == (1 << key_to_idx.size()) - 1) {
                                return dist[nx][ny][mask | (1 << idx)];
                            }
                            q.emplace(nx, ny, mask | (1 << idx));
                        }
                    }
                    else {
                        int idx = key_to_idx[tolower(grid[nx][ny])];
                        if ((mask & (1 << idx)) && dist[nx][ny][mask] == -1) {
                            dist[nx][ny][mask] = dist[x][y][mask] + 1;
                            q.emplace(nx, ny, mask);
                        }
                    }
                }
            }
        }
        return -1;
    }

private:
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
};