# 882. 细分图中的可到达节点

给你一个无向图（原始图），图中有 n 个节点，编号从 0 到 n - 1 。你决定将图中的每条边细分为一条节点链，每条边之间的新节点数各不相同。

图用由边组成的二维数组 edges 表示，其中 edges [i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi 之间存在一条边，cnti 是将边细分后的新节点总数。注意，cnti == 0 表示边不可细分。

要细分边 [ui, vi] ，需要将其替换为 (cnti + 1) 条新边，和 cnti 个新节点。新节点为 x1, x2, …, xcnti ，新边为 [ui, x1], [x1, x2], [x2, x3], …, [xcnti+1, xcnti], [xcnti, vi] 。

现在得到一个新的细分图，请你计算从节点 0 出发，可以到达多少个节点？如果节点间距离是 maxMoves 或更少，则视为可以到达。

给你原始图和 maxMoves ，返回新的细分图中从节点 0 出发可到达的节点数。

示例 1：

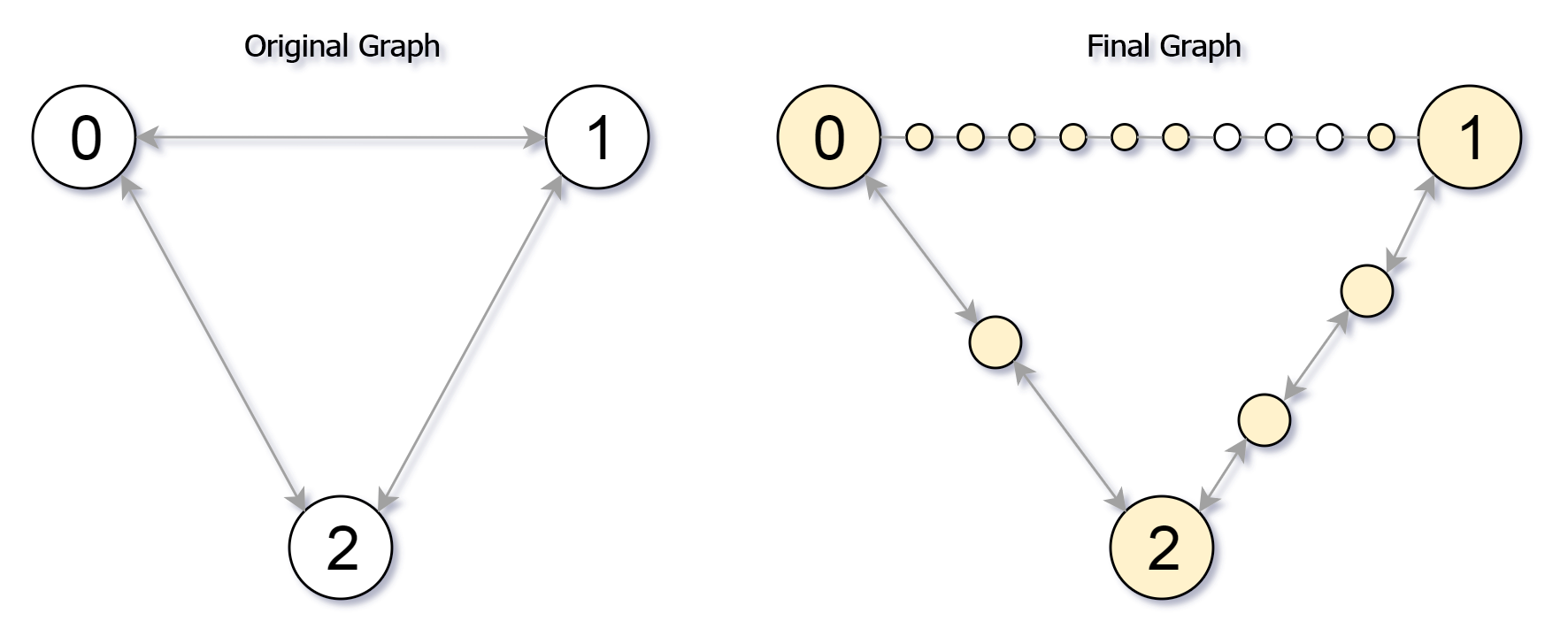
输入：edges = [[0,1,10],[0,2,1],[1,2,2]], maxMoves = 6, n = 3
输出：13
解释：边的细分情况如上图所示。
可以到达的节点已经用黄色标注出来。

示例 2：

输入：edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], maxMoves = 10, n = 4
输出：23

示例 3：

输入：edges = [[1,2,4],[1,4,5],[1,3,1],[2,3,4],[3,4,5]], maxMoves = 17, n = 5
输出：1
解释：节点 0 与图的其余部分没有连通，所以只有节点 0 可以到达。

提示：

0 <= edges.length <= min(n * (n - 1) / 2, $10^4$)
edges[i].length == 3
0 <= $u_i$ < $v_i$ < n
图中不存在平行边
0 <= cnti <= $10^4$
0 <= maxMoves <= $10^9$
1 <= n <= 3000

# 题解

class Solution {
public:
    int encode(int u, int v, int n) {
        return u * n + v;
    }

    int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
        vector<vector<pair<int, int>>> adList(n);
        for (auto &edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            adList[u].emplace_back(v, nodes);
            adList[v].emplace_back(u, nodes);
        }

        unordered_map<int, int> used;
        unordered_set<int> visited;
        int reachableNodes = 0;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.emplace(0, 0);
        while (!pq.empty() && pq.top().first <= maxMoves) {
            auto [step, u] = pq.top();
            pq.pop();
            if (visited.count(u)) {
                continue;
            }
            visited.emplace(u);
            reachableNodes++;
            for (auto [v, nodes] : adList[u]) {
                if (nodes + step + 1 <= maxMoves && !visited.count(v)) {
                    pq.emplace(nodes + step + 1, v);
                }
                used[encode(u, v, n)] = min(nodes, maxMoves - step);
            }
        }

        for (auto &edge : edges) {
            int u = edge[0], v = edge[1], nodes = edge[2];
            reachableNodes += min(nodes, used[encode(u, v, n)] + used[encode(v, u, n)]);
        }
        return reachableNodes;
    }
};